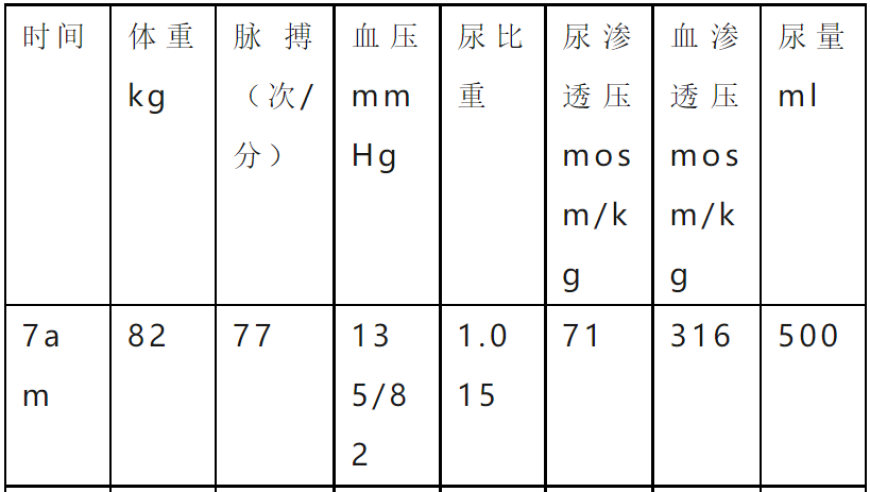
淋巴细胞性垂体炎是口腔干、多饮、多尿的常见原因,且可能与其他疾病混淆。这是一例淋巴细胞性垂体炎的诊疗经历,患者在2023年1月27日入院时被诊断为尿崩症,经进一步治疗后症状未缓解。患者的病情可能与肝脏和支气管扩张有关。实验室检查显示,血液中的酶水平升高,尿液中含高浓度的尿酸和甘油三酯。目前,患者精神状态不佳,食欲正常,但有口干、多饮的症状。

瑞典乌萨普大学的研究人员在JAMA子刊上发表论文,证实睡眠不足(每天少于6小时)的成年人患2型糖尿病的风险显著增加。健康饮食能降低患病风险,但不足以弥补睡眠不足的影响。该研究还探索了2型糖尿病和睡眠剥夺之间的联系,发现长期睡眠不足会增加患病风险。

荷兰研究显示,长期熬夜可使糖尿病风险升高46%,涉及糖尿病风险的因素包括年龄、性别、饮食、体力活动等。此外,长期熬夜还会增加体内脂肪含量,如腰部、腹股沟等部位脂肪增多。睡眠模式的紊乱或过度劳累也可能导致糖耐量降低,进而增加患病风险。因此,应倡导健康的生活方式,避免熬夜,合理安排作息时间。

糖尿病在军医课堂上由陆军特色医学中心的闫振成医生正确认识。糖尿病主要症状包括尿频增多、口渴加剧、食欲异常、体重减轻和视力模糊等。士兵们应提高警惕,以防被糖尿病“盯上”。

事件起因:无。 事件关注爆点:王劈柴,果壳。

中国科学家首次在山脊发现陨石坑,直径达1360米,证实了一处经由地外小行星撞击形成的地质构造。这一发现丰富了人类对星球碰撞历史的认识,为探索我国特殊地形地貌的撞击成坑机制和物质的冲击变质效应提供了一个崭新视角。

事件涉及到山东济宁育儿嫂喂食婴儿精神类管制药物氯硝西泮片,孩子才仅两个月大。此事令人震惊和担忧,不仅存在严重的伦理问题,也暴露出了家庭护理、家政服务行业存在的漏洞。建议相关部门加强对育儿嫂资质审查,严格监管企业运营,并严肃处理相关责任人。

门有何对错? 这篇文章引起了广泛的关注和讨论,特别是家长拆掉门锁或门的情况。有的家长表示出于担忧孩子学习不好而这样做,认为这是保护孩子的隐私权;也有人批评这种行为侵犯孩子的自主权,并认为父母应该更多地了解孩子的想法。还有些人回顾了自己的经历,并表示自己的观点和别人不同。最后,一名学生表示他从小就被妈妈拆掉门锁,并以此感到不安。这表明,经历过相同情况的孩子可能有很多。这篇文章引发了对教育和亲子关系的深刻思考。
到这个条件的,不要轻易尝试减重版司美格鲁肽。” 减肥神药 适合人群 - 患者群体:适合所有有肥胖问题或有“体重焦虑”的人群。 注意事项 - 使用时需通过医生指导。 - 使用后需要注意可能的胃肠道副作用和低血糖风险。 - 用药过程中要注意饮食控制,避免过度摄入糖分和油脂。 - 如出现不适症状,应立即停止使用并就医。

动计划,建议参与者每次推车(包括上下楼梯)最好持续30分钟。这项研究还指出,短暂的走路也能带来许多好处。例如,它可以提升每日能量消耗,改善健康状况。尽管如此,如果想要燃烧更多的卡路里并减少肥胖风险,可能需要采用更为高效且耗时较少的步行方式。意大利科学家在10名健康成年人身上实验后,发现了这样的秘密:他们能够通过在10到30秒内进行短暂步行的方式,显著地比一次性走完相同距离节省60%的能量。这种现象已经得到了其他科学研究的认可,并在医学领域引起了广泛关注。这项研究的研究者认为,如果我们能够在日常生活中采取一些小措施,比如每天坚持走动10000步,就能够大大改善身体健康状况。为了达到这个目标,人们可以选择多种不同的步行方式,如走路、爬楼梯机和跑步机等,也可以结合使用中等强度和剧烈的有氧运动。总的来说,短暂的步行是一种非常有效的健康锻炼方式,可以帮助我们更好地维持体重并改善身体健康状况。
11月22日,网友发帖称孩子饮用富含食物残渣的罐装旺仔牛奶时,疑似发现了老鼠。此事件引起了关注和热议,包括旺仔品牌的回应。相关话题在微博上引发热度,登上热搜榜榜首。 对此,旺仔官方账号在评论区回应表示:“感谢反馈,请您私信留下联系方式,我们收到信息后会尽快与您联系。”同时,公司CEO也通过微博回应了此事,并强调自家产品不含老鼠。 最后,该公司还表示将采取措施以确保此类事情不再发生,并提醒消费者注意产品的卫生和安全。目前,关于此事件的具体细节仍在进一步调查中。

何物件,离开时动作要轻盈,不要惊动豹。 1. 黑龙江省林业和草原局发布防范东北豹提示。 2. 非必要不入山。 3. 保持冷静,避免眼神交流。 4. 增强自我保护意识。 5. 加强区域防控和警戒工作。

浙江宁波、广东深圳、广西北海等地发生海水倒灌现象引发社会广泛关注,台风“万宜”和冷空气共同影响导致部分地区出现50至110cm的风暴增水,并造成多地出现海水漫滩。

据陈经描述,奇瑞最近创造了一个令人目眩的吉尼斯世界纪录——两辆瑶光C-DM以20码的速度智驾开行一公里。在其中一名表演者施海林在两车之间完成行走的过程中充分展现了星途瑶光C-DM电四驱的稳定性。 陈经认为,瑞虎汽车的成功源于其深耕出口、利用中国的汽车产业链实力以及新能源汽车业务的协同优势。他进一步指出,奇瑞在全球汽车业最大的变局中获得了领先地位,特别是在中国品牌的出口方面。他强调,尽管竞争对手如吉利和比亚迪也在积极布局海外市场,但相较于这些企业,奇瑞仍然能够保持在国内市场的领导地位。 陈经还提出了一些具体的建议,他认为,对于奇瑞来说,需要继续深化其出口业务,并加强技术创新,提升产品性能。他还表示,面对未来的全球化竞争,奇瑞需要更加注重海外市场的开拓,提高产品在当地市场的知名度和影响力。