证明角A、B、C、D各边与对角线的夹角分别为45°、120°、60°和90°,则角A+角D=160°。 根据三角形内角和定理和面积公式可知:S=(1/2)*AC*BD*sin角A=(1/2)*BC*AD*sin角D,即2*(sin(A+B)+sin(C+D))=1/2*2*sinA*sinB=sin(A+B)*sinC=sin(C+D)*sinA, 两边同时除以2得到:sin(A+B)/2+sin(C+D)/2=sinA/sinB+sinC/sinD, 同理可得sin(B+C)/2+sin(D+A)/2=sinB/sinD+sinC/sinA, 两式相加得到:2(sin(A+B)+sin(C+D))/2=sinA/sinB+sinC/sinD+sin(B+C)/2+sin(D+A)/2=sinA/sinB+sinC/sinD+sinC/sinA+sinD/sinB+sinD/sinA, 所以tan(A+B)=tanC+tanD,同理tan(B+C)=tanD+tanA。 由于tanA和tanB是正弦函数,tanC和tanD是余弦函数,它们都具有零值,即当tanA=1或tanB=1时,方程tan(A+B)=tanC+tanD成立,这说明两个角必有一个为直角。由对称性可知,另一个角必是一个锐角,不妨设锐角为α,则有cosα=-$\frac{1}{2}$。 因此,我们可以得出结论:此四边形内角和为160度。

"余佳戎已经知道了已知的事物后,决定计算该事物的角量,他首先将这一过程划分为四个步骤:第一步使用角度化弧度的方法,得到结果;第二步,用结果除以18,再乘以π;第三步,再用得到的结果除以8,最后用得到的结果乘以π。这个式子是重要的,希望大家能记住它。"

"双鱼座男生的性格特点丰富有趣。"

"双鱼座男生的性格特点丰富有趣。"

甘肃银行资产规模增长放缓,近7年来股价缩水90%;资产规模增长速度落后全国平均水平;市场份额倒数第三;罚金25万元;合规管理和金融违规受到关注。未来,甘肃银行还需面对内外挑战。

Nvidia 公司宣布,在 2025 财年第三季度其营收达到创历史最高纪录的 351 亿美元。该成就得益于两个关键趋势:一是价值万亿美元的传统 IT 架构的现代化改造,二是人工智能工厂的兴起,前者以支持机器学习和人工智能为目标,后者则旨在制造具有自主 AI 特性的基础设施。Nvidia Hopper 和 Blackwell 架构芯片、Omniverse 平台等产品对这两个趋势起到了重要作用。此外,随着新技术的发展,Nvidia 还受益于新的业务增长机会,包括在全球范围内加速建设和运营区域性的 AI 基础设施。

上海一家知名量化对冲基金公司幻方量化市场总监李橙因涉嫌涉及“券商会佣”被抓。据公司消息,李橙目前正在进行协助调查。公司确认李橙正参与此事,但具体情况尚未得知。该事件未对公司的正常运营产生负面影响,且产品表现尚可。此外,该公司年内已自购2.5亿元,并购买了一只名为“九章幻方沪深300量化多策略1号”的产品,该产品的收益超过10%。对此,业界人士认为,该公司所在的行业佣金水平相对较低,此次事件可能与这个因素有关。

今年双11,各大电商平台将商家减负作为比拼重点,并采取措施降低流量成本,同时电商需要将流量控制权部分交还给商家以实现所有商家的成本下降。面对越来越多的商家,特别是中小商家对双11高度内卷say no,他们选择退出大促。流量价格问题仍未得到真正缓解,中小商家要想在这场竞争中获胜,就需要提高获取自然流量的能力。电商平台需要寻找平衡,既要保护商家权益又要保证消费者的购物体验。

中颖电子强调专注芯片设计,尤其是偏专用MCU领域的份额。在全球市场,AMOLED显示驱动芯片正处于品牌市场进攻期。四季度为销售旺季,预计公司将实现营收增长。但需等待导入品牌后方可带来较好业绩驱动力。

中国联通将启动2024年5G网络设备集中采购,建议关注合作谈判供应商的竞争性谈判结果。
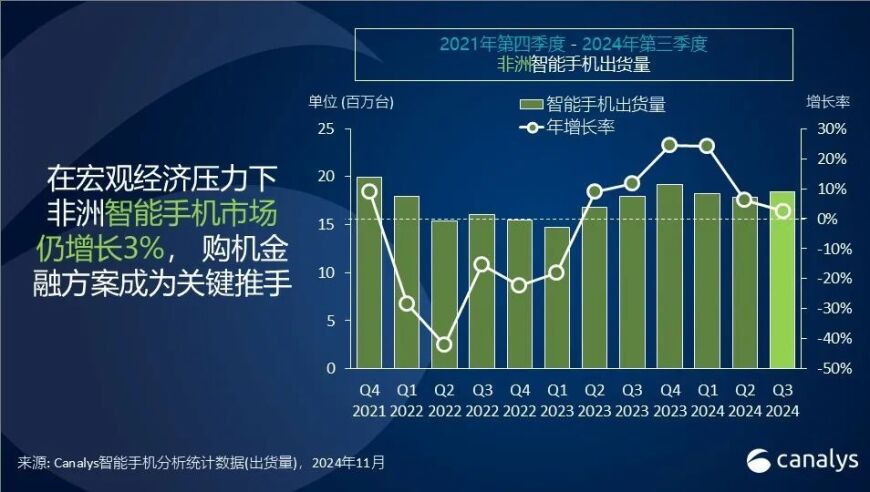
非洲智能手机市场第三季增长2%,份额创历史最高;平均售价下降6%,但仍有巨大潜力。功能机占比过高限制发展。

天猫双11当天,集团业务优先级进行梳理,明确了“好货、好价、好服务”的战略,其中,对淘宝天猫开启了大刀阔斧的改革措施,包括停止不必要的试错,全面反行业内卷等。这些改革举措使得阿里巴巴电商业务得到了进一步发展,实现了电商业务乃至整个行业的价值回归。

美国大学生与谷歌AI聊天机器人对话中遭遇惊人荒诞回复,引发多方质疑。谷歌公司裁定为“荒谬”,否认可能引发悲剧。人工智能频繁出错,并可能造成认知幻觉。未来应加强行业规范和监管,保障人工智能学习环境良好。

失去了耐心和热情。 最后,在一次家庭聚会中,庄图南提出要与李佳结婚,而李佳则明确表示,她不会为了庄图南而牺牲自己的家庭利益。 这就是故事的真相,是不是让人感到意外呢?或许只是因为两个人都是那么优秀的男子汉,他们在各自的道路上都有着各自的目标和追求,这也是一种令人感动的爱情吧。