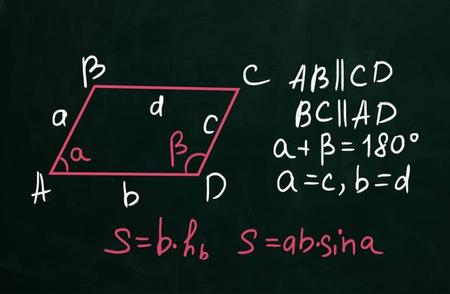
"通过多种方法,如三角函数、勾股定理等,人们证明了四边形内角和等于360度这一基本定理。"

"余佳戎已经知道了已知的事物后,决定计算该事物的角量,他首先将这一过程划分为四个步骤:第一步使用角度化弧度的方法,得到结果;第二步,用结果除以18,再乘以π;第三步,再用得到的结果除以8,最后用得到的结果乘以π。这个式子是重要的,希望大家能记住它。"

"科一科二科三科四分别考什么?"和"驾照科目一二三四分别是什么驾驶证?"是两句话,它们的共同点是都在询问驾照考试的内容。另外,这两句话都强调了交通法规的重要性,并且提到了四个科目——道路交通安全法律、法规及相关只是考试、场地驾驶技能考试、道路驾驶技能考试、以及安全文明常识考试。总的来说,这两句话都是在询问驾照考试的具体内容和重要性。

中印近期达成的解决方案涉及撤退一线部队,主要包括停火、交涉、安置临时居民等措施。 信息来源:玉渊谭天.rich_media_content。

邓超孙俪儿子罕见同框,背后故事引热议;等等小花成为焦点,母亲孙俪全力支持丈夫新片宣传。

美国至少20个州的非洲裔居民收到了含有种族歧视内容的短信,其中一些短信指派他们去做摘棉花的工作。这些短信被误认为是对他们的侮辱,而并非真事。种族歧视在美国仍然是一个问题,没有真正改变。

人之一拉迪卡与父母一起登上了印度版《企业家》杂志的封面。其中,她已准备好接手父亲创办的公司,被认为是家族业务的积极参与者,并且在全球范围内拓展业务。她出生于一个拥有巨大财富的家族,同时具有深厚的商业知识和投资能力。虽然看起来文静贤淑,但实际上是一位富有挑战精神的女性,毕业于哈佛商学院。她曾表示希望通过教育和继续学习来丰富自己的人生经历,并期待为社会做出更大的贡献。

瑞士首位使用自杀舱自杀身亡:根据荷兰报纸《Volkskrant》报道,一位名为菲利普・尼奇克博士开发的Sarco自杀舱被证明能够为绝症患者提供具有尊严和无痛性结束生命的方式。2017年9月,美 国女 人成为世界 第一 个使用自杀舱的人。据 法医 认证,死者的脖子受了重伤,经颅底骨髓炎可能与此有关。公司拒绝证实上述报道,并称苏黎世报纸援引颅底骨髓炎为原因提出死亡的可能性。目前该公司正在进行刑事调查,包括对所有被捕人员的释放。

最近一个兄弟逆袭成功,通过隐藏宝藏和打书得到珍贵装备,但也花掉大量资金。另一个兄弟遭遇新手陷阱,买到假冒商品并损失惨重。最后,主播马头头成功打造一只全红金绕僧,但还需继续努力追全红。喜欢的同学可以关注、分享和收藏。

魔神坛斗士是一部改编自原作《铠传》的日本漫画,因其强大的人物塑造和剧情吸引而备受瞩目。其中的鬼魔将阿拉戈四魔将实力强大,同时又具有强烈的复仇精神,特别是剧中饰演的那哑挫角色,智商高、战斗经验丰富,但形象却给人一种冷酷无情的感觉。另外,暗魔将恶奴弥守和幻魔将螺咒罗也各有特点,但在总体上,他们都展现了出色的战斗技巧和人格魅力。

Uzi参加传奇杯后陷入困境,老OMG上单Gogoing、中单无状态只剩两人,多名解说质疑传奇杯官方立场。最终, MLXG助力Uzi在关键时刻选中了西门夜说,Uzi粉丝大受鼓舞。

拿下了五场比赛的胜利,并且在第四场的比赛中以4-1击败了KSG,晋级到总决赛。这一战的胜利为AG超玩会带来了巨大的荣誉,并且也打破了KSG战队在KPL赛事中的无敌记录。尽管这个结果并不如预期,但AG超玩会展现出了他们的实力和毅力,证明了他们是今年最强的队伍之一。AG超玩会的胜利也让我们看到了KPL赛事的魅力和精彩。我们期待他们在未来的比赛中能够继续保持这样的高水平表现。

当前全球汽车市场呈现稳定增长态势,其中新能源汽车尤其引人关注。中国在2024年新能源汽车市场的表现异常抢眼,占全球市场份额近六成。欧洲和北美市场也在加大投入推广新能源汽车,但总体来看,中国仍占据主导地位。各国对新能源汽车的推动政策不断优化,有望进一步提高新能源汽车的普及率。

截至11月7日24点,小鹏P7+收获31528台大定订单。小鹏P7+有多成功呢?这个数据超过了小鹏过往所有的纪录,而之前被认为“爆款”的MONA M03,达到3万大定用了48小时。未来周末,随着到店看车、试驾的潜客增加,P7+的订单还有望迎来第二波增长高峰。虽然最终P7+给出的上市价格还未公布,但其成功已无需过多解读,因为其背后是对科技的追求和对品质的坚持。小鹏汽车通过全新SoC解析技术,提升了0.6km的续航里程,使得P7+具备极高的能耗表现。它的成功证明,即使面对激烈的市场竞争和价格战,也能保持产品的核心竞争力。