
下库小学下库小学的陶艺课堂已经成为了每周五下午校本课程,该课程吸引了5年级学生参与,并帮助他们培养了自己的审美观和创造力。陶华老师带领该校学生创作了许多陶器艺术品,其中包括花瓶、半浮雕人物形象和小房子等。目前,陶华老师的特色课程已经在启明小学得到了认可,并有望推广到更多农村地区的小学。

青岛崂山区沙子口街道小河东幼儿园秉持"温馨家园 幸福成长"的办园宗旨和"愉悦和谐 正向发展"的工作理念,致力于为山里孩子提供优质的学前教育,包括胡同文化课程、幼小衔接活动、家园活动和早教公益课堂等。这些活动深受家长和社区好评,同时也为孩子们提供了丰富的亲子互动机会,让他们在快乐中学习,在健康中成长。

临澧县推动学前教育提升,重点建设一批“县中心幼儿园为龙头、乡镇中心幼儿园为骨干、村级幼儿园为依托、公办幼儿园为主体、民办幼儿园为补充”的新型学前教育格局。这些举措帮助许多孩子在家门口享受到优质的普惠资源,使学前教育更加均衡发展。此外,临澧县还实施了3期学前教育三年行动计划,有效提升了学前教育的质量和影响力。李雨初书记表示,临澧县对学前教育非常重视,并且看到了明显的成效。

徐州徐海路幼儿园发布园内劳动生活课视频引发了广泛热议,该视频展示了幼儿园小朋友熟练进行各种劳动技能的情况,引起了广大网友的好评。该幼儿园还提供了丰富的物资支持,如柴火等生活材料,许多家长也自发送来了生活材料。此举旨在培养幼儿的兴趣爱好,并提高其动手能力,增强亲子关系的和谐。随着生活水平的提高,家长开始更加重视劳动教育,认为与其将重心放在学习外语等文化知识上,不如让孩子亲身体验劳动的魅力。此外,该幼儿园的做法也为其他地区提供了一个可借鉴的模式。

中美瑞康研发的FUS基因靶向小干扰RNA(RAG-21)疗法获美国FDA孤儿药资格,用于治疗肌萎缩侧索硬化症(SLSD),已有两款相关药物已在中国上市。 此为中美瑞康携手蔡磊推进的第二款针对SLSD的小核酸药物,RAG-17主要用于治疗由SOD1基因突变引起的成肌萎缩侧索硬化症(ALS),目前该疗法已在5月申请临床试验默示许可,并将于近期公布更多信息。
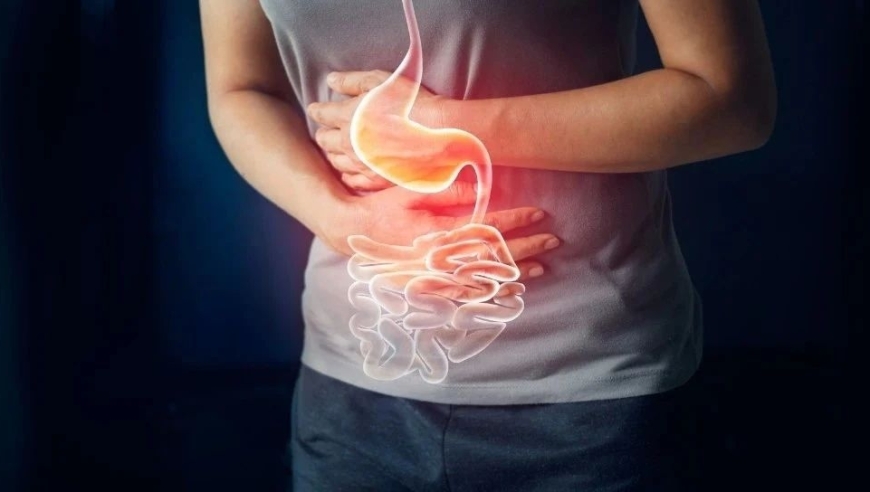
功能性胃肠病是一种无法解释的躯体症状,主要表现在恶心、呕吐、腹泻、便秘等方面,尤其在年轻人和女性中更为常见。一般认为,情绪会影响胃肠健康,部分患者是因为长期心情不好,导致消化系统功能受到影响。根据相关文献,功能性胃肠病的全球患病率为40%,中国的人群患病率也在逐年增长。如果经过多种检查排除了各种器质性疾病,并且病程超过半年且症状没有加重的趋势,就可以诊断为功能性胃肠病。消化内科是治疗功能性胃肠病的主要科室,其中约一半的患者属于功能性胃肠病。

湖南怀化“理发师晓华”通过改变饮食结构、养成良好生活习惯、正确洗发护发等方式成功摆脱大油头,不少网友表示头皮控油工作终于告一段落,重新焕发生机。

据研究,睡姿和口臭有直接关系。长期张嘴或打呼噜会导致口干舌燥,增加唾液分泌量,进而引发口臭。同时,熬夜、压力增大、饮食不规律以及心情低落等都可能引起疲劳并产生口臭。 综上所述,保持良好的生活习惯和饮食习惯对于减少口臭至关重要。如果你的口臭问题持续存在,应及时就医检查,以确定病因并采取相应的治疗措施。

一款医用卫生巾会被质疑“偷工减料”,多款知名品牌卫生巾内吸收层长度明显低于其标称值,且卫生巾市场价格相对较高。据统计,女性一生中有2535天是经期,每过一天需要使用5片卫生巾。业内普遍认为,医用卫生巾应严格按照国家标准进行生产,并保障产品质量安全。
1. 美国乙肝疫苗公司VBI Vaccines宣布破产,暂停运营。 2. 渣股上市公司腾盛博药引进PreHevbrio在亚太区及澳大利亚、新加坡等地。 3. VBI破产将导致腾盛博药失去PreHevbrio的独家开发权,但仍会独立研发BRII-179。 4. 没有影响后续的临床试验。 5. 合作伙伴Vir正在进行各种联合治疗方案的研究,并有望获得更多数据。 6.腾盛博药已经回应称将撤回PreHevbrio。 7. BRII-179仍将继续独立研发。 8. 尚未确定是否会重启项目。

哈佛研究人员证实吃不同蔬果对预防慢性病有显著效果,包括钾、镁、β-胡萝卜素、类黄酮和膳食纤维等营养成分。这些蔬果含糖量较低,可通过抗氧化、抗炎、降血压等多种方式降低患慢性病风险。同时,合理烹调蔬果也会降低其营养价值。选择多种颜色的新鲜蔬果,注意清洗、切割、蒸煮等烹饪方式,并遵循十六字原则。

中国有5个城市攀升至全球科研城市前列 本文报道指出,在线发布《自然》增刊“2024自然指数-科研城市”中,2023年全球十大科研城市分别为北京、上海、纽约都市圈、波士顿都市圈、南京、旧金山湾区、巴尔的摩-华盛顿、广州、武汉和东京都市圈。 其中,北京自2016年以来一直是科研城市的头号强人,增长率达到近9%;上海以2023年的排名提升至第二位;南京和武汉也有着稳定的提升。 文章认为,中国城市特别是省会城市,在多个领域已取得显著进步,成为全球科研中心的竞争者。 此外,《自然》增刊还着重研究了不同学科领域的数据,并揭示了中国各大城市的科技实力。如中国有8个城市晋升化学领域十强城市,物理科学和地球与环境科学领域各有6座中国城市位列前列。 值得注意的是,尽管中国的科学研究整体水平已经相对较高,但在某些领域仍存在差距,如医疗科学领域,仍有部分城市无法与美国相比。

SpaceX星舰第六次综合测试飞行试验取得成功,飞船顺利完成首次“在轨点火试验”并降落在印度洋预定海域。特朗普与马斯克分别前往现场观看。这次试飞距离上次第五次试飞间隔仅一个月,但也出现了助推火箭B13降落海面后发生爆炸的情况。此次试飞标志着SpaceX新一代星舰S31的成功研发,有望在未来承担更大的任务。同时,NASA计划在此基础上进一步研究和改进其发动机。
福建省多个高校已公布寒假时间,大多数高校寒假时间为29天到37天,部分高校寒假从1月中旬开始至2月底结束。具体信息可参考相关高校官网。